Abstract
Reconstructing a 3D scene from unordered images is pivotal in computer vision and robotics, with applications spanning crowd-sourced mapping and beyond. While global Structure-from-Motion (SfM) techniques are scalable and fast, they often compromise on accuracy. To address this, we introduce a principled approach that integrates gravity direction into the rotation averaging phase of global pipelines, enhancing camera orientation accuracy and reducing the degrees of freedom. This additional information is commonly available in recent consumer devices, such as smartphones, mixed-reality devices and drones, making the proposed method readily accessible. Rooted in circular regression, our algorithm has similar convergence guarantees as linear regression. It also supports scenarios where only a subset of cameras have known gravity. Additionally, we propose a mechanism to refine error-prone gravity. We achieve state-of-the-art accuracy on four large-scale datasets. Particularly, the proposed method improves upon the SfM baseline by 13 AUC@1deg points, on average, while running eight times faster. It also outperforms the standard planar pose graph optimization technique by 23 AUC@1deg points. The code is at here.
Video
Experiments
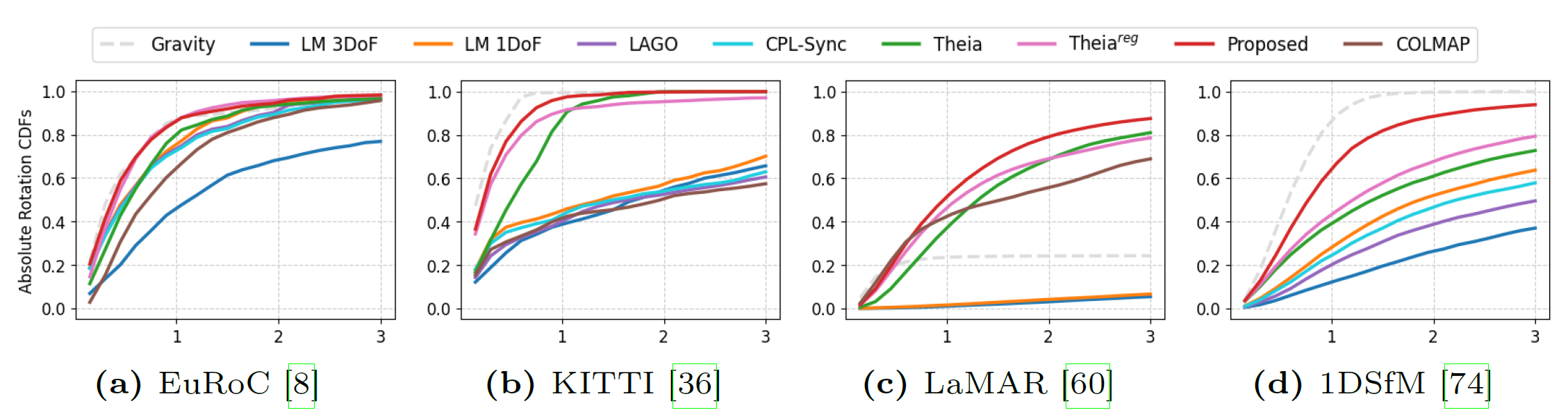
Real World Experiments
For EuRoC and KITTI, gravity directions for all images are measured by IMU.
For LaMAR dataset, only gravity directions for mobile phone images are used.
For 1DSfM dataset, ground truth vertical directions with extra gaussian noise are used as gravity directions.
Synthetic Experiments
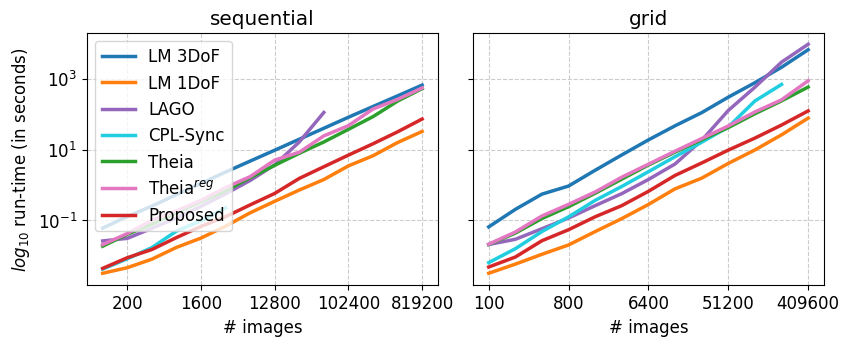
To show the scalability of our method, we conducted synthetic experiments.
We deployed two configurations: images connected sequentially and images connected in a grid.
For both setups, our method scaled easily up to hundreds of thousands of images, and it was orders of magnitude faster than other baselines.
Sensitivity Analysis
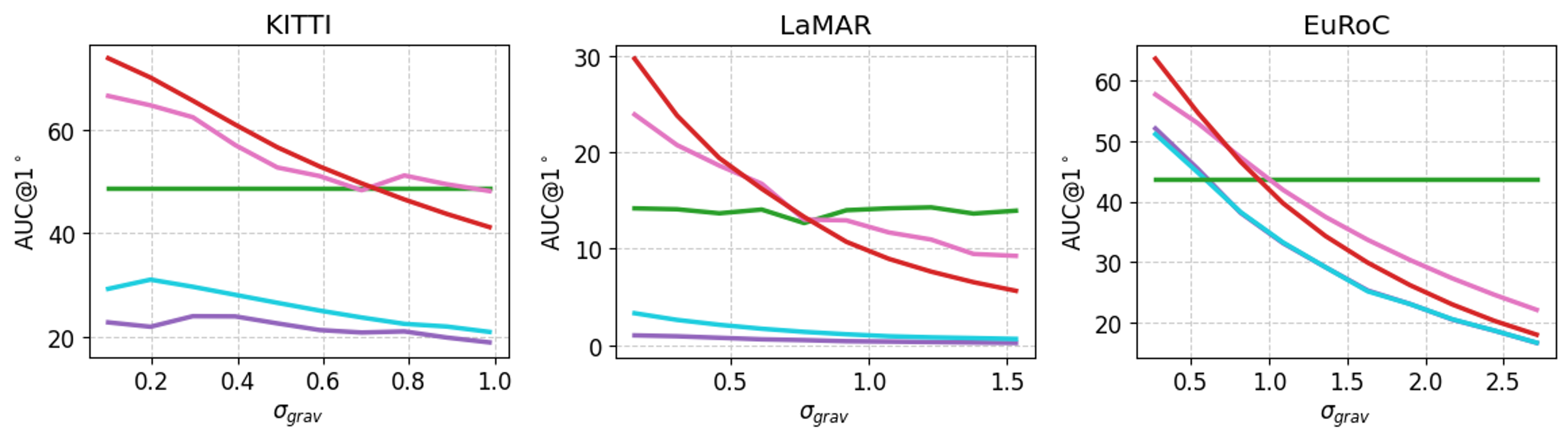
With respect to gravity noise
Alternating gravity noise by interpolation between measurement and ground truth.
Rotation averaging with 1 degree-of-freedom remains better performance until about 0.7 degree of error
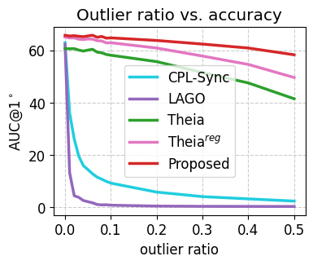
With respect to outlier ratio
Our method performs well under 50% of outliers